Cerita dan Matematika
Sabtu, 04 Juni 2022
Daya Matematika Menurut Histori, Konsep, Riset, Aplikasi
Rabu, 01 Juni 2022
Daya Matematika Level Filsafat dan Psikologi
A. PENDAHULUAN
Pembelajaran yang baik termasuk pembelajaran matematika adalah pembelajaran yang mencapai tujuannya. Untuk mencapai tujuannya, suatu pembelajaran haruslah bermakna yang dilakukan selain melalui aktivitas juga dengan kegiatan tanya jawab. Kegiatan menanya selain dapat meningkatkan kreativitas dengan kemungkinan memunculkan pertanyaan-pertanyaan dibalik suatu pertanyaan yang membentuk suatu eksponensial, juga mampu mengukur tingkat perhatian siswa dalam pembelajaran. Untuk dapat menanya perlu berbagai informasi yang diketahui dan hal yang hendak dikaitkan atau diuji kebenarannya. Dalam matematika, kemampuan matematika atau daya matematika seseorang berpengaruh pada keberhasilan dalam pembelajaran matematika. Kemampuan matematis didefinisikan oleh NCTM (1999) sebagai kemampuan dalam mengeksplorasi, melakukan konjecture dan argumentasi logis dalam menyelesaikan permasalahan tidak rutin, mengkomunikasikan melalui bentuk matematis dan menghubungkan ide-ide pada matematika dengan disiplin ilmu yang lain. Terdapat banyak komponen dari daya matematika ditinjau dari keilmuannya seperti aljabar, numerik, statistik, kalkulus, geometri, dan sebagainya namun perlu juga diperhatikan aspek filosofis dan psikologisnya.
Matematika sebagai suatu keilmuan memiliki objek langsung dan objek tak langsung. Objek langsung meliputi fakta, postulat, aksioma, konsep, prinsip, dan prosedur. Sedangkan obyek tak langsung meliputi kemampuan memecahkan masalah, kemampuan menalar, kemampuan mengkomunikasikan, kemampuan menghubungkan, dan kemampuan representasi. Kemampuan pemecahan masalah meliputi kemampuan memahami konsep dan menggunakan prosedur dalam mencari solusi dari permasalahan matematika. Kemampuan menalar meliputi kemampuan dalam menghubungkan fakta-fakta untuk menarik suatu kesimpulan. Adapun aktivitas yang tercakup di dalam kegiatan penalaran matematik meliputi: menarik kesimpulan logis; menggunakan penjelasan dengan menggunakan model, fakta, sifat-sifat, dan hubungan; memperkirakan jawaban dan proses solusi; menggunakan pola dan hubungan; untuk menganalisis situasi matematik, menarik analogi dan generalisasi; menyusun dan menguji konjektur; memberikan lawan contoh (counter example); mengikuti aturan inferensi; memeriksa validitas argument; menyusun argument yang valid; menyusun pembuktian langsung, tak langsung dan menggunakan induksi matematik.
Sementara itu kemampuan komunikasi matematis (mathematical communication) merupakan kesanggupan atau kecakapan siswa untuk menyatakan dan menafsirkan gagasan matematis secara lisan, tertulis atau mendemonstrasikan apa yang ada dalam persoalan matematika dan juga kemampuan untuk mendemonstrasikan dan manafsirkan gagasan atau ide matematika dari suatu uraian ke dalam model matematika (grafik, diagram, tabel dan persamaan). Kemampuan koneksi matematik adalah kemampuan yang ditunjukkan siswa dalam mengenali representasi ekuivalen dari konsep yang sama, mengenali hubungan prosedur matematika suatu representasi ke prosedur representasi yang ekuivalen, menggunakan dan menilai keterkaitan antar topik matematika dan keterkaitan di luar matematika, menggunakan matematika dalam kehidupan sehari-hari. Kemampuan representasi matematis adalah salah satu standar proses yang perlu ditumbuhkan dan dimiliki siswa.
B. ASPEK FILOSOFIS
Aspek dasar filosofis suatu ilmu termasuk matematika adalah ontologi, epistimologi, dan aksiologi. Setiap metode filosofis memiliki tempat tersendiri dalam kegiatan memecahkan masalah matematika, seperti metode Apriori dan Aposteriori.
1. Metode Apriori
Metode apriori tanpa percobaan dapat digunakan dalam statistik, yakni mengetahui peluang tanpa melakukan percobaan terlebih dahulu. Contoh berapa peluang munculnya kartu king dalam 2 kali pengambilan kartu tanpa pengembalian? Jika diketahui bahwa peristiwa A dapat muncul dalam m cara dan total seluruh kemungkinan peristiwa adalah n, maka peluang munculnya peristiwa A: P(A)=m/n.
2. Metode Aposteriori
Metode aposteriori dapat digunakan dalam statistik seperti pada contoh jika peristiwa serupa A muncul m kali dalam total percobaan n, maka peluang pengamatan P(A)=m/n. Ini berarti diasumsikan percobaan telah dilakukan dengan memperoleh peluang pengamatan. Bila dalam 80 kali pelemparan mata uang (yang tak harus seimbang) munculnya Angka sebanyak 45 kali (sisanya Gambar sebanyak 35 kali), maka P (munculnya Angka) = 45/80. Setelahnya maka menggunakan pengalaman tersebut sebagai dasar dalam menentukan pengalaman baru.
Selain terdapat metode yang dapat diimplementasikan dalam setiap cabang ilmu matematika, dalam aspek filosofis terdapat logika dan pengalaman. Logika memiliki unsur-unsur yakni analitik dan apriori. Unsur analitik saling melengkapi dengan apriori, jika apriori adalah kemampuan mengetahui yang belum terjadi maka analitik disini berfungsi untuk menimbang dan menggali kebenaran dari apriori dengan berbagai hal yang memiliki keterkaitan. Seseorang yang daya matematikanya kuat, logikanya pasti kuat dan analitiknya juga kuat. Sementara itu unsur dari pengalaman adalah sintetik aposteriori. Sintetik dan aposteriori juga saling melengkapi dalam hal saling mengaitkan antara pengetahuan yang telah dimiliki dengan yang baru saja diperoleh melalui hubungan sebab akibat sehingga paham setelah kejadian. Benjamin Bloom telah mengklasifikasikan tingkat kemampuan berpikir seseorang, bahwa sebelum direvisi oleh Anderson (2001) tingkatan tertinggi dalam kemampuan berpikir adalah sintesis lalu diikuti evaluasi. Evaluasi disini bermakna memberikan keputusan atau judgment.
Kemampuan berpikir seseorang ada kaitannya dengan kemampuan memahami realita fenomenologi dimana unsurnya adalah reduksi dan idealisasi. Reduksi adalah kemampuan untuk bisa melihat sedangkan idealisasi adalah kemampuan dalam menyimpulkan. Sebagai contoh seseorang dapat naik kereta api dan melihat fenomena kereta tersebut berjalan cepat atau lambat sehingga dengan membandingkan waktu tempuh naik kereta dengan baik bus dapat disimpulkan mana yang lebih cepat. Dari unsur-unsur logika dan pengalaman, pengaruhnya dalam pembelajaran matematika tentu sangat banyak. Seseorang dengan kemampuan apriori dan analitik yang baik tentu akan dapat sedikit menerawang dan memiliki kemampuan bermain logika dalam pikirannya seperti contoh mengenai mahasiswa yang diajak studi tour ke candi Borobudur lalu diminta melakukan analisa keterkaitannya dengan etnomatematika. Mahasiswa dengan kemampuan apriori yang baik akan segera berpikir mengenai hal apa saja yang perlu dipersiapkan dan diamati lantas dipadukan dengan analitik yang baik berdasarkan aposteriori yang dimiliki untuk menghasilkan suatu sintesis yang baik mengenai keterkaitan etnomatematika dalam bentuk candi borobudur seperti konsep perhitungan volume batu yang digunakan, bentuk arsitektur agar dapat berdiri kokoh di atas bukit, serta bentuk ornamen-ornamen yang memiliki keindahan namun tetap tersusun dengan baik,
Selanjutnya dalam pembelajaran matematika menurut Shigeo Katagiri perlu memperhatikan konten dan metodenya. Setiap konten tentu memiliki metode berbeda untuk mempelajarinya, apakah dengan deduktif atau induktif. Pengemasan konten yang menarik dengan metode yang sesuai akan dapat membuat siswa lebih mudah dalam mempelajari sehingga memiliki kontribusi besar pada daya matematika yang dimiliki siswa. Komponen matematika yang terdiri dari Fakta, Postulate, Aksioma, Teorema, Prinsip memiliki cara-cara dalam mengajarkannya. Salah satunya adalah dengan pendekatan Realistik yang membawa matematika dari aspek konkret menuju formal dengan fenomena didaktis di dalamnya. Dalam tahapan mempelajarinya perlu conjecture dan convince menurut Profesor Kaye Stacey yakni hubungan yang logis dan dapat dibuktikan.
C. ASPEK PSIKOLOGIS
Dari aspek psikologi, kemampuan seseorang dalam mengolah informasi itu berbeda-beda termasuk di dalamnya terdapat strategi agar mudah mengingat atau menyimpan informasi seperti dengan membuat skema-skema atau singkatan-singkatan, namun juga terdapat faktor lupa. Salah satu hal penting dalam aspek psikologi belajar adalah perhatian dan hubungan antara pengetahuan awal dan informasi baru. Perhatian akan membantu seseorang untuk fokus pada 1 hal, karena manusia tidak dapat fokus dalam banyak hal sekaligus. Selain itu, dengan materi yang terlalu banyak seseorang dapat mengalami cognitive overload walaupun dalam beberapa fakta mengatakan seseorang yang berdaya matematika kuat maka memiliki perhatian dan ketahanan belajar yang kuat pula.
DAYA MATEMATIKA: Pendahuluan
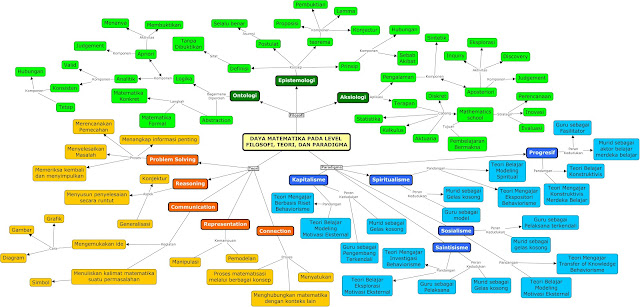
Daya matematika yakni mathematical power yang berbeda dengan power of mathematics. Daya matematika tidak dapat dilepaskan dari filsafat ilmu yakni pada aspek ontologi (makna), aspek epistemologi (cara mempelajarinya), dan aspek aksiologi (kebermanfaatan suatu ilmu). Daya matematika atau mathematical power diibaratkan sebagai titik tengah di antara hulu dengan hilir yang dapat menentukan apakah seseorang yang belajar ilmu matematika (hulu) dapat mencapai tujuan dari belajar matematika tersebut (hilir). Daya matematika mencakup pengetahuan akan makna dari ilmu matematika, strategi mempelajari dan memecahkan masalah, serta mampu menggali potensi dari ilmu matematika yang merupakan power of mathematics.
Sebagai contoh dari power of mathematics adalah terciptanya alat bantu hitung dari suatu algoritma yakni kalkulator dan komputer, terciptanya berbagai alat elektronik dan otomotif berdasarkan perhitungan yang mengkombinasikan fisika dan matematika, terciptanya berbagai macam obat atau antivirus yang mencegah perkembangbiakan virus secara cepat dan berkelipatan. Daya matematika adalah suatu potensi yang dimiliki oleh setiap orang dalam hal memperoleh ilmu matematika dan menjadi ahli untuk menerapkan keilmuan tersebut di dalam kehidupan sehari-hari. Untuk memiliki daya matematika tentu dapat dengan melatih literasi matematika seperti kemampuan memecahkan masalah, menalar, komunikasi, dan menghubungkan. Melatih literasi matematika dapat melalui pendugaan dan penemuan, mengajukan suatu permasalahan atau pertanyaan, maupun eksplorasi.
Pada aspek kemampuan memecahkan masalah, seseorang dapat dibimbing dalam hal melihat informasi yang berkaitan dengan apa yang ditanyakan berdasarkan teori Vygotsky mengenai Zona Proximal Development yakni berdasarkan tingkat kebutuhan bantuan sampai dapat mandiri memecahkan suatu permasalahan. Akan lebih baik apabila permasalahannya bukan hal yang rutin. Pada aspek menalar, seseorang dapat dilatih dengan tipe soal berbasis High Order Thinking Skill (HOTS) sehingga dapat menganalisa, mengevaluasi, bahkan menciptakan hal baru dari suatu hal. Pada aspek komunikasi, seseorang dapat dilatih untuk mengemukakan ide atau mengkonstruksi bentuk matematis dari suatu langkah penyelesaian masalah. Pada aspek menghubungkan, seseorang dapat dilatih dengan berbagai permasalahan yang saling memiliki keterkaitan baik berbagai subyek dalam suatu ilmu maupun berbagai subyek dari berbagai keilmuan yang berbeda.
Sebagai pendukung dalam upaya meningkatkan daya matematika seseorang, pemilihan sumber belajar juga harus diperhatikan agar dapat memfasilitasi aktivitas. Perbantuan media belajar seperti Augmented Reality, video pembelajaran, aplikasi seperti GeoGebra, Autograph, Desmos dapat membantu siswa dalam melatih kemampuan visualisasi dari suatu konsep seperti Geometri, Kalkulus, Aritmatika, Statistika, dan lain sebagainya. Penggunaan alat bantu perhitungan juga diharapkan dapat membuat siswa berlatih untuk mempertajam kemampuan berpikir kritis dan kreatif.
Senin, 06 Desember 2021
Inovasi Dalam Pembelajaran Matematika
I. PENDAHULUAN
A. Latar Belakang
Perkembangan peradaban pada abad 21 tidak dapat terlepas dari peran teknologi yang hadir pada banyak aspek seperti kebutuhan pokok, pendidikan, bisnis perdagangan, keuangan, kesehatan, informasi, transportasi, dan gaya hidup. Teknologi hadir sebagai sebuah inovasi dalam membantu mempermudah dan memenuhi kebutuhan hidup manusia namun memerlukan literasi informasi dan berpikir kritis yang baik. Terjadi pergeseran paradigma terhadap klasifikasi kebutuhan hidup manusia dimana kebutuhan pokok yang tadinya hanya pangan, sandang, dan papan, pada saat ini teknologi dapat termasuk ke dalam kebutuhan pokok. Pandemi Covid-19 yang melanda dunia sejak akhir tahun 2019 sampai saat ini memberikan dampak signifikan pada seluruh aspek kehidupan. Penerapan protokol kesehatan membuat segala aktivitas yang sebelumnya dilakukan dengan tatap muka beralih melalui teleconference atau platform penyedia layanan dalam jaringan (daring). Platform teleconference dan aplikasi dalam jaringan sebenarnya sudah banyak berkembang bahkan sebelum adanya Pandemi Covid-19, namun tidak semua orang mengetahuinya apalagi manggunakannya.
Sebuah survei dari lembaga Sirclo dalam (Rakhmawati et al., 2021) menunjukkan adanya peningkatan signifikan dalam penggunaan aplikasi online (Shopee, Tokopedia, Lazada, Bukalapak, dan Blibli) dalam kegiatan jual-beli di Indonesia pada kuartal kedua tahun 2020 sebanyak 255 juta pengguna dibandingkan kuartal 1 tahun 2020 sebanyak 227 juta pengguna. Pemerintah melalui (Kemdikbud, 2020) juga mengeluarkan Surat Edaran No.4 tahun 2020 mengenai Pelaksanaan Kebijakan Pendidikan di masa Covid-19 yang mengharuskan pembelajaran tatap muka dilakukan secara daring. Pembelajaran matematika yang merupakan sebuah aktivitas sosial dan bermakna dalam mengkonstruksi pengetahuan tentu memerlukan strategi dan media inovatif yang dapat memfasilitasi kegiatan observasi, praktik, diskusi, dan evaluasi secara daring.
Meskipun dilaksanakan secara daring, pembelajaran perlu memperhatikan aspek baik kompetensi yang akan dicapai, kemampuan kognitif dan afektif siswa, kondisi psikologis siswa, materi yang diajarkan, dan fasilitas. Pembelajaran inovatif menurut (Methkal & Algani, 2019) perlu memperhatikan 5 aspek yakni memfasilitasi pembelajaran konstruktif, menggunakan berbagai metode pembelajaran dan penilaian, memperhatikan perbedaan gaya mengajar terhadap siswa, menggunakan media dan aplikasi digital, serta melakukan penilaian untuk proses pembelajaran. Beberapa contoh strategi pendekatan pembelajaran matematika inovatif seperti Realistic Mathematics Education (RME), Open-Ended, Science Technology Engineering Mathematics (STEM), Problem Based Learning (PBL), Project Based Learning, Blended Learning, Guided Discovery, Learning Trajectory, Ethnomathematics, dan Scientific. Media pembelajaran berbasis teknologi yang dapat membantu pembelajaran secara inovatif dapat berupa augmented reality, comic book, games application, e-learning module, dan lembar kerja siswa (LKS) berbasis digital.
Dengan memperhatikan karakteristik dari setiap cabang keilmuan dan keterkaitan dengan cabang materi yang lainnya, pelaksanaan pembelajaran matematika yang konstruktif, interaktif, dan memfasilitasi kreativitas, kejujuran, serta menyenangkan, dapat dengan mengkombinasikan antara model pendekatan dengan media dan sumber tertentu. Pemilihan model pembelajaran juga dapat disesuaikan dengan fasilitas yang ada dan tidak terpaku pada ketersediaan teknologi digital sehingga dapat menggunakan banyak sumber lain bahkan dapat berdasarkan kearifan lokal seperti membelajarkan matriks dengan bentuk anyaman bambu.
B. Tujuan
Dengan memahami kebutuhan akan keterampilan abad 21 yang harus dimiliki oleh manusia, pembelajaran matematika dapat dilakukan dengan mengintegrasikan aspek-aspek atau indikator dari keterampilan abad 21 ke dalam muatannya. Untuk itu perlu diperhatikan dalam pemilihan model pembelajaran, media dan sumber yang digunakan, proses pembelajaran, dengan materi yang dipelajari sehingga dapat menciptakan inovasi yang berbeda yang belum pernah dialami siswa. Model penilaian juga dibuat dengan berbagai cara dan rubrik penilaian sehingga siswa tidak merasa bosan dan cemas akan model penilaian yang lama.
II. PEMBAHASAN
A. Model Pembelajaran
1. Open-Ended
Pendekatan Open-Ended (dalam pembelajaran matematika) adalah pembelajaran yang menghadirkan permasalahan-permasalahan yang memiliki banyak jawaban benar dan cara mencari jawaban atau disebut juga incomplete problem (Shimada & Becker, 1997). Permasalahan Open-Ended dapat memberikan kebebasan pada siswa untuk aktif melakukan aktivitas dalam melatih intuisinya yang berkaitan dengan berpikir, kreativitas, kemampuan matematisasi, investigasi, dan komunikasi, serta memungkinkan penilaian lebih objektif karena memberikan kesempatan siswa menjawab satu atau lebih jawaban benar dibandingkan pembelajaran matematika yang dilakukan secara ekspositori (Sullivan et al., 2000).
Menurut Sawada dalam (Shimada & Becker, 1997), terdapat 3 tipe problem pada pendekatan Open Ended yakni mencari hubungan, mengklasifikasikan, dan mengukur. Melalui beberapa tipe problem dalam pendekatan Open Ended diharapkan siswa dapat mencari dan menemukan aturan serta hubungannya, mengklasifikasikan berdasarkan perbedaan karakteristik untuk menemukan konsep, dan melakukan penghitungan berdasarkan permasalahan dengan mengaplikasikan pengetahuan atau konsep dan keterampilan yang diperoleh sebelumnya. Berikut adalah contoh permasalahan Open Ended dalam pembelajaran matematika:
“Diketahui luas persegi panjang adalah 24 cm2, berapa cm ukuran panjang dan lebarnya? Jawaban dari pertanyaan tersebut ada banyak dibandingkan dengan pertanyaan seperti berapakah luas suatu persegi panjang yang memiliki panjang 6 cm dan lebar 4 cm?”
Untuk mempermudah penerapan pendekatan Open Ended dalam pembelajaran matematika, perlu dijelaskan fase pendekatan Open Ended yakni:
a. Membuat suatu permasalahan
Permasalahan dalam dibuat atraktif, menarik, dan memiliki banyak cara serta solusi. Konteks permasalahan sebaiknya disesuai dengan tingkat perkembangan siswa dan siswa diberikan banyak waktu untuk mengeksplorasi. Tujuan dalam memberikan permasalahan ini adalah untuk menunjukkan bahwa siswa perlu mempelajari dan memahami konsep agar dapat menyelesaikan permasalahan. Contoh permasalahan kontekstual:
Jarak stasiun A dan B adalah 357km. Sebuah kereta cepat berjalan dari stasiun A dan sebuah kereta lokal berjalan dari stasiun B. Dalam 3 jam kedua kereta tersebut bertemu. Jika kecepatan kereta cepat adalah 79km/jam, berapa kilometer lebih sedikit kereta lokal tersebut menempuh jarak dalam 1 jam dibandingkan kereta cepat? Untuk tingkatan lebih sulit dan lebih Open Ended, pertanyaan bisa juga diganti dengan: Jika kecepatan kereta cepat lebih dari 3 kali kecepatan kereta lokal, berapa kilometer lebih sedikit kereta lokal tersebut menempuh jarak dalam 1 jam dibanding kereta cepat?
b. Mengorganisir pembelajaran
Membuat suasana belajar agar semua siswa terlibat aktif dalam pembelajaran melalui tahap matematisasi permasalahan, mencari aturan dan hubungan matematis menggunakan bahasa dan pengetahuan siswa sendiri, memecahkan masalah, dan memeriksa pekerjaan yang dapat dilaksanakan dalam kelompok maupun individu. Tahapan ini merupakan tahapan yang krusial dalam upaya
c. Mencatat respons dari siswa
Siswa mempresentasikan hasil pekerjaannya. Hasil dari presentasi setiap kelompok/siswa dibandingkan baik dari ide langkah penyelesaian maupun jawaban untuk memperkaya pengetahuan semua siswa. Dengan ini guru bisa melakukan penilaian terhadap proses belajar dan keterlibatan siswa dalam pembelajaran.
d. Membuat kesimpulan dari apa yang sudah dipelajari siswa
Siswa diajak untuk menyampaikan kesimpulan dengan cara guru memberikan bantuan atau pancingan kecil untuk menggabungkan setiap pendapat sesuai dengan poin-poin menuju konsep yang dipelajari.
Berdasarkan penjelasan di atas, Pendekatan Open-Ended memiliki keunggulan:
a. Siswa aktif dalam kegiatan dan dapat mengemukakan idenya
b. Siswa berkesempatan menggunakan pengetahuan dan keterampilan matematis
c. Siswa dengan kemampuan rendah dapat mencoba menyelesaikan permasalahan dengan cara yang diketahuinya sendiri
d. Siswa termotivasi melakukan mencari tahu dan mencoba serta dapat menghargai usaha dan kegagalan
e. Siswa menjadi kaya pengalaman dalam menemukan konsep, menemukan kesenangan dan motivasi ketika sudah menemukan konsep, serta memperoleh pengakuan dari rekannya
Meskipun memiliki keunggulan, Pendekatan Open Ended juga memiliki kekurangan:
a. Sulit dalam membuat permasalahan kontekstual dan bermakna terkait matematika
b. Siswa kesulitan memahami dalam merespons dan menjawab pertanyaan
c. Siswa dengan kemampuan tinggi dapat menjadi cemas dan tidak percaya diri terhadap jawabannya
d. Siswa mungkin merasa kurang nyaman karena mengalami kesulitan dalam menarik kesimpulan dari pembelajaran
Meskipun memiliki kekurangan, namun tetap dapat diminimalisir dengan membuat desain pembelajaran yang memfasilitasi semua siswa, memotivasi seluruh siswa, dan guru banyak menambah literasi mengenai permasalahan Open Ended. Keunggulan penggunaan pendekatan Open Ended dapat diketahui melalui beberapa penelitian yakni pendekatan Open-Ended dapat meningkatkan kemampuan siswa pada beberapa aspek seperti keterampilan berpikir tingkat tinggi pada siswa (HOTS) karena memiliki validitas yang sangat baik nilai rata-rata dari validator mencapai 3.42, kemampuan kolaboratif siswa terutama dalam hal berargumentasi ketika menyelesaikan permasalahan, kemampuan komunikasi siswa, kemampuan berpikir kreatif matematis, dan penalaran siswa (Chan & Clarke, 2017), (Fatah et al., 2016), (Kurniawan et al., 2018), (Kurniawati et al., 2020), (Viseu & Oliveira, 2012), (Yanti et al., 2018). Pendekatan Open Ended dapat diterapkan pada berbagai tingkat pendidikan seperti SD, SMP, SMA, maupun Universitas.
2. Problem Based Learning (PBL)
Suatu model pembelajaran yang menuntut siswa untuk berfikir kritis, memecahkan masalah, belajar secara mandiri, dan menuntut keterampilan berpartisipasi dalam tim. Proses pemecahan masalah dilakukan secara kolaborasi dan disesuaikan dengan kehidupan. Inti dari Problem Based Learning (PBL) adalah menyajikan situasi terkait masalah kontekstual dan bermakna yang dapat memfasilitasi kegiatan investigasi dan penemuan konsep. (Arends and Kilcher, 2010). Langkah-langkah pelaksanaan PBL adalah sebagai berikut:
a. Menyajikan permasalahan
Menyiapkan permasalahan kontekstual yang sering dijumpai oleh siswa dalam kehidupan sehari-hari. Permasalahan dapat dibuat beragam tidak hanya terbatas pada jual beli dan untung rugi yang sering muncul.
b. Merencanakan penyelidikan
Siswa memahami permasalahan untuk menyusun langkah penyelesaiannya yang dapat dilakukan dalam satu kelas langsung maupun dalam kelompok kecil. Dalam tahapan ini guru membantu dengan memberikan bantuan ringan terkait hal-hal yang akan dilakukan siswa seperti mencari informasi terkait permasalahan. Proses ini diharapkan dilakukan secara otentik berdasarkan pengetahuan siswa.
c. Melakukan penyelidikan
Siswa mencoba melakukan penyelidikan dan memecahkan permasalahan berdasarkan rencana dan informasi yang diperoleh yang dapat dilakukan dengan melakukan eksperimen percobaan. Siswa mengaitkan hasil yang diperoleh dengan konsep formal. Sementara itu guru melakukan observasi dan membantu siswa agar tidak terlalu melenceng dari konsep.
d. Mengembangkan dan menyajikan hasil karya
Siswa mempresentasikan hasil penyelidikannya yang diharapkan terdapat banyak variasi proses mengkonstruksi konsep. Guru bertindak sebagai moderator.
e. Menganalisis dan mengevaluasi proses pemecahan masalah
Siswa bersama-sama dengan guru menyimpulkan hasil pembelajaran dan bagaimana menemukan konsep yang dipelajari melalui langkah-langkah yang efektif dari informal menuju formal.
Keunggulan dari PBL diantaranya pembelajaran menjadi lebih bermakna dengan siswa mengkonstruksi ilmu dari pengetahuannya, membantu siswa dalam mengembangkan kemampuan penalaran, siswa dapat mengembangkan pengetahuan bersamaan dengan keterampilan secara simultan, dan meningkatkan kemampuan berpikir kritis. Beberapa penelitian menunjukkan bahwa pembelajaran matematika dengan PBL dapat meningkatkan hasil belajar siswa, meningkatkan kemampuan pemecahan masalah, pemahaman, minat belajar siswa, dan kemampuan berpikir kreatif (Amalia, et.al., (2017); Malmia, et.al., (2019); Meke, et. al., (2018); Tan, et. al., (2020)).
3. Problem Posing
Problem Posing merupakan suatu strategi pembelajaran yang dapat mengaktifkan siswa sehingga mampu menggali pengetahuan mereka dan mengeksplorasi materi pembelajaran dengan mengajukan masalah (Mishra & Iyer, 2015). Dalam pelaksanaannya, siswa didorong untuk mengajukan pertanyaan dari permasalahan yang ada (Dwita & Sugiman, 2020). Terdapat 3 macam Problem Posing berdasarkan situasi pembelajaran menurut Silver (dalam Mahmudi, 2011) yakni:
a. Pre-Solution Problem
Permasalahan diberikan pada awal pembelajaran dengan menyajikan sebuah ilustrasi atau grafik yang mana siswa diminta untuk membuat pertanyaan terkait ilustrasi tersebut. Pertanyaan dapat dibebaskan atau dibatasi berdasarkan kebutuhan materi pembelajaran. Berikut adalah contoh dari permasalahan:
“Diberikan suatu grafik yang menunjukkan rekor waktu (dalam detik) dari perenang pria dan wanita dalam kejuaraan renang dunia 100 meter dari tahun 1912 sampai tahun 2020. Garis-garis itu menunjukkan kecenderungan perubahan rekor waktu dari perenang pria dan perenang wanita dari tahun ke tahun. Guru dapat meminta siswa membuat pertanyaan terkait permasalahan tersebut.”
Beberapa pertanyaan yang mungkin muncul adalah bagaimana perbandingan perubahan dari waktu ke waktu rekor antara perenang pria dan perenang wanita? Manakah yang memiliki gradien lebih besar?”
b. Within Solution Problem
Siswa diminta untuk menyampaikan pertanyaan dalam rangka menyelesaikan suatu permasalahan terkait pemahaman konsep. Pertanyaan dibatasi pada konteks seputar materi yang dipelajari. Berikut adalah contoh dari permasalahan:
“Sebanyak 20.000 galon air diisikan ke kolam renang dengan kecepatan tetap. Setelah 4 jam pengisian, isi kolam renang tersebut menjadi 5/8 nya. Jika sebelum pengisian kolam tersebut telah terisi seperempatnya, berapakah kecepatan aliran air tersebut?”
Beberapa pertanyaan yang mungkin timbul seperti: Berapa galon air di kolam renang ketika kolam itu berisi seperempatnya? Berapa galon air di kolam renang Ketika kolam renang itu berisi 5/8 nya? Berapa rata-rata perubahan banyaknya air di kolam renang itu? Berapa waktu yang diperlukan untuk mengisi kolam renang tersebut sampai penuh?
c. Post Solution Problem
Untuk meningkatkan pemahaman konsep, siswa diminta memodifikasi tujuan permasalahan yang telah diselesaikan melalui pertanyaan-pertanyaan. beberapa teknik yang dapat digunakan untuk membuat pertanyaan pada tipe ini adalah mengubah informasi atau data pada soal semula, menambah informasi atau data pada soal semula, mengubah nilai data yang diberikan, tetapi tetap mempertahankan kondisi atau situasi soal semula, dan mengubah situasi atau kondisi soal semula, tetapi tetap mempertahankan data atau informasi yang ada pada soal semula. Contoh persoalan terkait tipe ini adalah sebagai berikut: sebuah persegi memiliki luas 25 cm2. Pertanyaan yang dapat dimunculkan adalah? bagaimana luasnya jika sisinya diperpanjang 2 kalinya? bagaimana luasnya jika sisinya ditambahkan 2 cm?
Beberapa penelitian menyampaikan bahwa Problem Posing dapat meningkatkan kemampuan pemecahan masalah, pemahaman konsep, penalaran, dan meningkatkan kemampuan berpikir tingkat tinggi (Cai, et. al., (2020); Dwita & Sugiman, (2020); Mahmudi, (2011)).
4. Realistic Mathematics Education (RME)
Realistic Mathematics Education (RME) atau pendidikan matematika realistik merupakan pendekatan pembelajaran yang menyajikan suatu masalah, yang mana permasalahan tersebut mampu dibayangkan oleh siswa atau permasalahan tersebut nyata dalam pikiran siswa sebagai pondasi dalam membangun konsep matematika sehingga dapat memunculkan ide baru, menghasilkan pemahaman yang lebh baik, berdasarkan pendekatan aksiomatis (Freudenthal dalam Gravemeijer & Trewel, 2000). Pendekatan RME memiliki 3 prinsip dalam implementasinya yakni:
a. Guided Reinvention
Menyajikan permasalahan yang sesuai dengan konsep yang dipelajari oleh ahli, sehingga melalui topik yang disajikan siswa harus diberi kesempatan mengalami sendiri proses yang sama dengan proses yang dilalui para ahli ketika konsep-konsep matematika ditemukan.
b. Didactical Phenomelogy
Menurut prinsip fenomena didaktik, situasi yang mejadi topik matematika diaplikasikan untuk diselidiki berdasarkan dua alasan; (1). Memunculkan ragam aplikasi yang harus diantisipasi dalam pembelajaran, dan (2). Mempertimbangkan kesesuaian situasi dari topik sebagai hal yang berpengaruh untuk proses pembelajaran yang bergerak dari masalah nyata ke matematika formal.
c. Self-Developed Models
Model matematika dimunculkan dan dikembangkan sendiri oleh siswa berfungsi menjembatani antara pengetahuan informal dan matematika formal, yang berasal dari pengetahuan yang telah dimiliki siswa.
Keunggulan dari penerapan RME diantaranya adalah memberikan pengertian dan operasional yang jelas antara keterkaitan matematika dengan kehidupan sehari-hari, proses konstruksi ilmu dari informal menuju formal melalui tahapan yang jelas, dan bersifat lengkap serta detail. Beberapa penelitian mengemukakan bahwa RME dapat meningkatkan kemampuan pemecahan masalah, membantu siswa dalam upaya kemandirian belajar, meningkatkan kualitas belajar dan mengajar, meningkatkan sikap afektif siswa terhadap matematika, meningkatkan prestasi belajar, dan kemampuan penalaran siswa (Hasibuan, et.al., (2019); Laurens, et. al., (2017); Saleh, et. al., (2018); Zakaria & Syamaun, (2017)).
5. Cooperative Learning
Pembelajaran kooperatif adalah strategi belajar dengan karakter utamanya berupa tugas, tujuan, dan pemberian reward dalam kelompok dengan syarat setiap siswa aktif dalam kegiatan diskusi, berargumen atau berdebat, dan kerja sama dengan tujuan utamanya adalah perkembangan kognitif yakni memperoleh informasi baru, menumbuhkan kerja sama dan meningkatkan keterampilan sosial siswa (Arends and Kilcher, 2010). Fase dalam pembelajaran kooperatif ada 6 yakni:
a) Menyampaikan tujuan dan motivasi pada siswa
Pada tahapan ini, peserta didik diharapkan dapat termotivasi dan fokus pada tujuan pembelajaran pada suatu materi misalkan pada materi konsep luas lingkaran sehingga siswa dalam kondisi siap untuk belajar kelompok.
b) Menyajikan materi
Dalam tahapan ini siswa diberikan suatu permasalahan yang akan dikerjakan dengan kerja sama untuk memperoleh informasi baru.
c) Mengorganisasi siswa dalam pembelajaran kelompok
Guru membagi siswa menjadi beberapa kelompok baik berdasarkan prestasi atau nomor urut ataupun secara acak.
d) Saling membantu dan bekerja sama dalam kelompok
Siswa berdiskusi dalam menyelesaikan permasalahan yang diberikan sementara itu guru sebagai fasilitator melakukan observasi dan membimbing apabila siswa mengalami kendala.
e) Mempresentasikan hasil pekerjaan
Siswa mempresentasikan hasil kelompoknya di depan kelas, sementara kelompok lain memberikan argumen. Guru berperan sebagai moderator sehingga diskusi tidak keluar jalur.
f) Memberikan penghargaan
Kelompok yang memperoleh pencapaian terbaik memperoleh penghargaan dari guru, sementara itu untuk yang belum berhasil diberikan motivasi.
Terdapat beberapa tipe pembelajaran kooperatif, yakni Student Teams Achievement Division (STAD), Jigsaw, Group Investigation, Numbered Heads Together (NHT), Think Pair Share (TPS), dan Team Games Tournament (TGT). Keunggulan pembelajaran kooperatif menurut (Kagan, 1994) diantaranya:
a) Siswa memiliki kepercayaan diri dalam mengemukakan pendapat
b) Siswa dapat bertoleransi dalam diskusi
c) Siswa bertanggung jawab dengan berkontribusi pada pekerjaan mandiri dan tim
Beberapa penelitian menyatakan bahwa pembelajaran kooperatif efektif dalam meningkatkan prestasi belajar, komunikasi matematis, kompetensi matematika, kemampuan pemecahan masalah, dan keterampilan sosial (Aguanta & Tan, (2018); Agustika, et al. (2019); Rattanatumma & Puncreobutr, (2016); Tahir, et al. (2020))
B. Media Pembelajaran
1. Lembar Kerja Siswa Terintegrasi dalam Live Worksheet
Lembar Kerja Siswa (LKS) bertujuan untuk memberikan instruksi dalam proses konstruksi ilmu melalui aktivitas di dalamnya. LKS memiliki keunggulan yakni dapat membuat siswa aktif dalam pembelajaran, membantu siswa dalam upaya mengkonstruksi pengetahuan, membantu meningkatkan pemahaman siswa, efektif dalam pencapaian kompetensi siswa, dan meningkatkan motivasi siswa (Ardina, 2016; Faizah & Astutik, 2017; Vitantri et.al, 2020).
Live Worksheet adalah sebuah aplikasi digital yang memungkinkan pembelajaran dilakukan dengan aktivitas dan interaktif melalui instruksi dan lembar kegiatan. Live Worksheet dapat diakses dengan menggunakan komputer, tablet, ataupun handphone. Beberapa penelitian mengungkapkan integrasi LKS ke dalam Live Worksheet dapat membantu pemahaman konsep pada siswa, membuat lebih efisien, membuat siswa aktif dan antusias (Amalia & Lestantyo, 2021; Andriyani et al., 2020). Selain itu, Live Worksheet juga mudah dioperasikan, fitur tidak rumit, tidak terlalu membutuhkan koneksi internet yang cepat, mampu mendokumentasikan hasil pekerjaan siswa, serta memungkinkan dilakukannya penilaian secara cepat dan akurat.
2. GeoGebra
GeoGebra adalah sebuah aplikasi untuk membantu visualisasi dalam pembelajaran Geometri maupun Aljabar. GeoGebra efektif dalam membantu siswa memahami konsep melalui praktik visualisasi, memfasilitasi pembelajaran online dengan interaktif, meningkatkan pengetahuan konsep dan prosedur, dan membuat pembelajaran menyenangkan (Em & Roman, 2020; Jusufi & Kitanov, 2019; Zulnaidi & Zamri, 2017). Penggunaan GeoGebra memiliki keunggulan seperti kemudahan akses melalui handphone atau komputer, ringan dan mudah dijalankan, memfasilitasi kegiatan eksplorasi siswa, serta memungkinkan untuk dilakukan observasi pada aktivitas siswa melalui GeoGebra Classroom yang dikelola guru.
3. Construct
Salah satu aplikasi yang dapat memadukan antara permainan dan pembelajaran adalah Construct. Construct terdapat 2 versi yakni Construct 2 dan Construct 3 yang memungkinkan media dibuat dengan database online maupun offline. Pembelajaran dapat diintegrasikan pada setiap tahapan permainan yang mana untuk menyelesaikan permainan, seorang pemain harus melalui tahapan pembelajaran juga baik dikemas dalam aktivitas maupun latihan soal. Construct memiliki keunggulan yakni tidak memerlukan algoritma yang rumit dalam pembuatannya karena sudah tersedia fitur desain baik berupa audio, video, gambar, url, maupun sketsa manual. Penggunaan Construct dalam pembelajaran terbukti efektif dalam meningkatkan motivasi, pemahaman konsep, dan pencapaian akademik (Setyaningrum & Waryanto, (2018); Suddin & Deda, (2020)).
4. Autograph
Sebagaimana GeoGebra, Autograph adalah sebuah aplikasi pembelajaran yang dapat menyajikan grafik, persamaan, maupun model geometri. Autograph memiliki keunggulan yakni lebih lengkap bila dibandingkan dengan GeoGebra serta fiturnya memudahkan pengguna dalam melakukan transformasi geometri. Penggunaan Autograph terbukti dapat meningkatkan komunikasi matematis siswa, kemampuan berpikir kritis, dan pemahaman konsep melalui eksplorasi dan menghubungkan konsep dengan pemodelan (Batubara, (2017); Kristianti, et. al., (2017); Triana, et. al., (2019)).
5. Quizizz
Quizizz Adalah sebuah aplikasi berbasis internet yang dapat digunakan untuk merancang kuis yang dapat dijadikan sebagai latihan atau evaluasi terhadap hasil belajar. Aplikasi ini memungkinkan guru dalam membuat soal dalam berbagai macam seperti pilihan ganda, jawaban singkat, maupun jawaban lengkap. Selain itu, pengaturan waktu juga dapat diatur dan proses monitor dapat dilakukan langsung oleh guru. Penggunaan aplikasi Quizizz untuk melakukan evaluasi terbukti efektif dalam meningkatkan kemampuan pemahaman konsep siswa karena untuk menjawab secara tepat dan cepat, siswa haruslah paham konsep dengan matang (Mulyati & Evendi, (2020); Pasco & Roble, (2020)).
C.
C. IMPLEMENTASI
Salah satu implementasi pendekatan Open-Ended dalam pembelajaran matematika adalah pada materi Geometri topik ketaksamaan segitiga. Menurut Battista dalam (Van de Walle et al., 2015) Geometri adalah sekumpulan konsep, langkah-langkah penalaran, dan sistem dalam merepresentasikan yang digunakan untuk mengeksplorasi dan menganalisa suatu bentuk dan ruang. Dalam Geometri, suatu bangun dapat terbentuk berdasarkan hubungan dari beberapa objek atau konsep. Setiap bangun memiliki karakteristik tersendiri sehingga dapat diklasifikasikan berdasarkan dimensi 2 maupun 3 dan sudutnya apakah konveks atau konkaf. Dengan pendekatan Open-Ended, siswa dapat menghubungkan, mengklasifikasikan, dan melakukan suatu perhitungan untuk menemukan suatu konsep dan prinsip. Berikut adalah implementasi pada pembelajaran mengenai ketaksamaan segitiga:
1. Membuat suatu permasalahan
Pada tahap ini guru menyiapkan suatu permasalahan
Perhatikan
gambar disamping! Buatlah bermacam-macam segitiga dengan menggunakan potongan
lidi yang berukuran kurang dari 10 cm dengan menuliskan sisi terpanjangnya di c
lalu ukurlah masing-masing besar sudutnya. Tuliskan hasilnya pada tabel di
bawah ini dan lengkapi tabel!
Selain menggunakan lidi, apabila fasilitas perangkat pembelajaran yang dimiliki siswa memadai, eksplorasi membuat segitiga dapat menggunakan aplikasi GeoGebra. Hasil eksplorasi siswa dipantau oleh guru melalui GeoGebra Classroom. Kemudian untuk perhitungan dalam melengkapi tabel dapat menggunakan bantuan Microsoft Excel.
2. Mengorganisir pembelajaran
Pembelajaran yang dilaksanakan secara daring menggunakan aplikasi Zoom mewajibkan siswa mengaktifkan kamera sehingga guru dapat melakukan observasi kegiatan siswa, sementara siswa melakukan eksplorasi dan menuliskan dalam tabel:
|
No |
Panjang Sisi |
a+b |
Besar Sudut |
Kuadrat Panjang Sisi |
a2+ b2 |
Jenis Segitiga |
||||||
|
a |
b |
c |
α |
β |
γ |
a2 |
b2 |
c2 |
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
SelaLKS dalam Live Worksheet, sementara guru memberikan sedikit instruksi jika siswa mengalami permasalahan atau kesulitan. Pertanyaan pada LKS untuk mengarahkan siswa pada penemuan konsep dibuat sedemikian hingga aspek mencari hubungan, mengklasifikasikan, dan mengukur dapat muncul seperti:
a. Dapatkah kita membuat segitiga dari 3 ruas garis dengan panjang yang sama dan dari 3 ruas garis dengan 2 ruas garisnya mempunyai panjang yang sama? Mengapa?
b. Dapatkah kalian membuat segitiga dengan ukuran sisi-sisi 2 cm, 3 cm, dan 5 cm?
c. Berdasarkan pengamatan kalian, berapakah jumlah sudut dalam segitiga?
e. Berdasarkan tabel di atas, bagaimana ciri-ciri segitiga lancip, segitiga siku-siku, dan segitiga tumpul?
3. Mencatat respons dari siswa
Pada kegiatan ini siswa menyampaikan hasil pekerjaannya kepada teman satu kelas. Guru dapat menunjuk secara acak atau mempersilahkan siswa untuk mengajukan diri mempresentasikan. Pada tahap ini pula guru mengajak siswa yang memiliki perbedaan jawaban atau cara mengerjakan untuk mengemukakan jawabannya. Pencatatan aktivitas yang dilakukan siswa juga dapat melalui GeoGebra Classroom dan Live Worksheet
4. Membuat kesimpulan dari apa yang sudah dipelajari siswa
Guru mengajak siswa untuk menarik kesimpulan dari hasil pekerjaan yang dipresentasikan menuju ke konsep konkret bahwa segitiga dapat terbentuk jika panjang sisi terpanjangnya kurang dari jumlah 2 sisi yang lainnya atau a + b > c. Jenis segitiga ditentukan oleh perbandingan antara kuadrat sisi terpanjangnya dengan jumlah kuadrat dari 2 sisi yang lainnya. Segitiga siku-siku dapat terbentuk jika nilai kuadrat sisi terpanjang sama dengan jumlah kuadrat dua sisi yang lain, segitiga lancip dapat terbentuk jika nilai kuadrat sisi terpanjang kurang dari jumlah kuadrat dua sisi yang lain, dan segitiga tumpul dapat terbentuk jika nilai kuadrat sisi terpanjang lebih dari jumlah kuadrat dua sisi yang lain.
III. DAFTAR PUSTAKA
Aguanta, E. R., & Tan, D. A. (2018). Effects of Dyad Cooperative Learning Strategy on Students’ Academic Performance and Attitude towards Mathematics. International Journal of English and Education, 7(3), 303-313.
Agustika, G. S., Aryati, N. M. A., & Wiarta, I. W. (2019). The Effectivity of TPS Type Cooperative Learning Model Based on Interpersonal Intelligence Toward Mathematical Knowledge Competencies. Journal of Education Research and Evaluation, 3(3), 147-156.
Amalia, A., & Lestyanto, L. (2021). LKS Berbasis Saintifik Berbantuan Live Worksheets untuk Memahamkan Konsep Matematis pada Aritmetika Sosial. Jurnal Cendekia : Jurnal Pendidikan Matematika, 5(3), 2911-2933. https://doi.org/10.31004/cendekia.v5i3.822
Amalia, E., Surya, E., & Syahputra, E. (2017). The effectiveness of using problem based learning (PBL) in mathematics problem solving ability for junior high school students. International Journal of Advance Research and Innovative Ideas in Education, 3(2), 3402-3406.
Andriyani, N., Hanafi, Y., Safitri, I., & Hartini, S. (2020). Penerapan Model Problem Based Learning Berbantuan LKPD Live Worksheet Untuk Meningkatkan Keaktifan Mental Siswa Pada Pembelajaran Tematik Kelas Va Sd Negeri Nogopuro.
Ardina, F. R. (2016). Lembar kerja siswa berbantuan geogebra sebagai upaya membantu pemahaman siswa materi limit fungsi aljabar. Jurnal Math Educator Nusantara: Wahana Publikasi Karya Tulis Ilmiah di Bidang Pendidikan Matematika, 2(1).
Arends, Richard I., & Kilcher, Ann. (2010). Teaching for Student Learning: Becoming and Accomplished Teacher. New York: Routledge.
Batubara, I. H. (2017). Peningkatan Kemampuan Pemahaman Konsep Matematis Melalui Model Pembelajaran Berbasis Masalah Berbantuan Autograph Dan Geogebra Di Sma Freemethodist Medan. MES: Journal of Mathematics Education and Science, 3(1), 47-54.
Cai, J., Chen, T., Li, X., Xu, R., Zhang, S., Hu, Y., ... & Song, N. (2020). Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design. International Journal of Educational Research, 102, 101404.
Chan, M. C. E., & Clarke, D. (2017). Structured affordances in the use of open-ended tasks to facilitate collaborative problem solving. ZDM - Mathematics Education, 49(6), 951–963. https://doi.org/10.1007/s11858-017-0876-2
Dwita, A., & Sugiman. (2020). Improving Problem-Solving Ability Through Problem-Posing Model in Mathematics. 491(Ijcah), 320–324. https://doi.org/10.2991/assehr.k.201201.057
Em, A. M. M., & Roman, A. G. (2020). Effectiveness of GeoGebra in Teaching Grade 10 Mathematics. Asian Journal of Multidisciplinary Studies, 3(2).
Faizah, H., & Astutik, E. P. (2017). Efektivitas lembar kerja siswa (LKS) berbantuan software geogebra pada materi program linier. Fibonacci: Jurnal Pendidikan Matematika dan Matematika, 3(2), 103-110.
Fatah, A., Suryadi, D., Sabandar, J., & Turmudi. (2016). Open-ended approach: An effort in cultivating students’ mathematical creative thinking ability and self-esteem in mathematics. Journal on Mathematics Education, 7(1), 9–18. https://doi.org/10.22342/jme.7.1.2813.9-18
Gravemeijer, K., & Trewel J. (2000). Hans Freudenthal: a mathematician on didactics and curriculum theory. Journal on Curriculum Studies, 32 (6), 777-796. https://doi.org/10.1080/00220270050167170
Hasibuan, A. M., Saragih, S., & Amry, Z. (2019). Development of Learning Materials Based on Realistic Mathematics Education to Improve Problem Solving Ability and Student Learning Independence. International electronic journal of mathematics education, 14(1), 243-252.
Jusufi, S., & Kitanov, S. (2019). Effectiveness of Using GeoGebra in Mathematics.
Kagan, S. (1994). Cooperative learning. San Clement, CA: Resources for Teachers.
Kemdikbud. (2020). SE No.4 tahun 2020 Pelaksanaan Kebijakan Pendidikan Dalam Masa Darurat Covid-19. Diambil dari https://www.kemdikbud.go.id/main/blog/2020/03/mendikbud-terbitkan-se-tentang-pelaksanaan-pendidikan-dalam-masa-darurat-covid19
Kristianti, Y., Prabawanto, S., & Suhendra, S. (2017, September). Critical thinking skills of students through mathematics learning with ASSURE model assisted by software autograph. In Journal of Physics: Conference Series (Vol. 895, No. 1, p. 012063). IOP Publishing.
Kurniawan, H., Putri, R. I. I., & Hartono, Y. (2018). Developing open-ended questions for surface area and volume of beam. Journal on Mathematics Education, 9(1), 157–168. https://doi.org/10.22342/jme.9.1.4640.157-168
Kurniawati, S., Budiyono, & Saputro, D. R. S. (2020). Open-ended mathematics module to improve students’ higher order thinking skill. Journal of Physics: Conference Series, 1613(1). https://doi.org/10.1088/1742-6596/1613/1/012068
Laurens, T., Batlolona, F. A., Batlolona, J. R., & Leasa, M. (2017). How does realistic mathematics education (RME) improve students’ mathematics cognitive achievement?. Eurasia Journal of Mathematics, Science and Technology Education, 14(2), 569-578.
Mahmudi, A. (2011). Problem Posing untuk Menilai Hasil Belajar Matematika. Matematika Dan Pendidikan Karekter Dalam Pembelajaran.
Malmia, W., Makatita, S. H., Lisaholit, S., Azwan, A., Magfirah, I., Tinggapi, H., & Umanailo, M. C. B. (2019). Problem-based learning as an effort to improve student learning outcomes. Int. J. Sci. Technol. Res, 8(9), 1140-1143.
Meke, K. D. P., Jailani, J., Wutsqa, D. U., & Alfi, H. D. (2019, February). Problem based learning using manipulative materials to improve student interest of mathematics learning. In Journal of Physics: Conference Series (Vol. 1157, No. 3, p. 032099). IOP Publishing.
Methkal, Y., & Algani, A. (2019). Innovative Ways to Teach Mathematics : Are they Employed in Schools ?, 7(14), 496–514. https://doi.org/10.18009/jcer.612199
Mishra, S., & Iyer, S. (2015). An exploration of problem posing-based activities as an assessment tool and as an instructional strategy. Research and Practice in Technology Enhanced Learning, 10(1). https://doi.org/10.1007/s41039-015-0006-0
Mulyati, S., & Evendi, H. (2020). Pembelajaran Matematika melalui Media Game Quizizz untuk Meningkatkan Hasil Belajar Matematika SMP. GAUSS: Jurnal Pendidikan Matematika, 3(1), 64–73. https://doi.org/10.30656/gauss.v3i1.2127
Pasco, J. C., & Roble, D. B. (2020). Mathematical Modelling Integrated With Dynamic GeoGebra Applications and Students’ Performance in Mathematics. Science International (Lahore), 32(2), 165–168.
Rakhmawati, N. A., Permana, A. E., Reyhan, A. M., & Rafli, H. (2021). Analisa Transaksi Belanja Online Pada Masa Pandemi Covid-19. Jurnal Teknoinfo, 15(1), 32. https://doi.org/10.33365/jti.v15i1.868
Rattanatumma, T., & Puncreobutr, V. (2016). Assessing the Effectiveness of STAD Model and Problem Based Learning in Mathematics Learning Achievement and Problem Solving Ability. Journal of Education and Practice, 7(12), 194-199.
Saleh, M., Prahmana, R. C. I., & Isa, M. (2018). Improving the Reasoning Ability of Elementary School Student through the Indonesian Realistic Mathematics Education. Journal on Mathematics Education, 9(1), 41-54.
Setyaningrum, W., & Waryanto, N. H. (2018). Developing mathematics edutainment media for Android based on students’ understanding and interest: A teachers’ review. Journal of Physics: Conference Series, 983(1). https://doi.org/10.1088/1742-6596/983/1/012093
Shimada, S., & Becker, J. P. (1997). The Open-Ended Approach: A New Proposal for Teaching Mathematics (5th ed.). Virginia: The National Council of Teacher of Mathematics, Inc.
Suddin, S., & Deda, Y. N. (2020). Education Game based on Timor Local Wisdom as an Android-Based Mathematics Learning Media. Al-Jabar : Jurnal Pendidikan Matematika, 11(2), 227–246. https://doi.org/10.24042/ajpm.v11i2.6958
Sullivan, P., Warren, E., & White, P. (2000). Students’ responses to content specific open-ended mathematical tasks. Mathematics Education Research Journal, 12(1), 2–17. https://doi.org/10.1007/BF03217071
Tahir, M., Tayeb, T., Rasyid, M. R., & Nur, F. (2020). The Cooperative Learning Comparison of Student Teams Achievement Division Type and Teams Assisted Individualization type Toward The Students’ Mathematical Communication Skill. Daya Matematis: Jurnal Inovasi Pendidikan Matematika, 8(2), 175-181.
Tan, S., Zou, L., Wijaya, T. T., & Dewi, N. S. S. (2020). Improving student creative thinking ability with problem based learning approach using hawgent dynamic mathematics software. Journal on Education, 2(4), 303-312.
Triana, M., & Zubainur, C. M. (2019). Students' Mathematical Communication Ability through the Brain-Based Learning Approach Using Autograph. Journal of Research and Advances in Mathematics Education, 4(1), 1-10.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2015). Elementary and Middle School Mathematics: Teaching Developmentally (Book) (9th ed.). Essex: Pearson Publication.
Viseu, F., & Oliveira, I. B. (2012). Open-ended tasks in the promotion of classroom communication in Mathematics. International Electronic Journal of Elementary Education, 4(2), 287–300.
Vitantri, C. A., Jayus, J., & Sholihah, M. (2020). Pengembangan LKS Untuk Memfasilitasi Pemahaman Konsep Matematis Siswa Pada Materi Aljabar. Jurnal Derivat: Jurnal Matematika dan Pendidikan Matematika, 7(1), 21-30.
Yanti, M., Hasratuddin, D., & Sitompul, P. (2018). Development of Teaching Materials Based On Open-Ended Approach with Autograph Assistance to Improve Mathematical Creative Thinking Ability of Junior High School, 200(2016), 298–303. https://doi.org/10.2991/aisteel-18.2018.65
Zulnaidi, H., & Zamri, S. N. A. S. (2017). The effectiveness of the GeoGebra software: The intermediary role of procedural knowledge on students’ conceptual knowledge and their achievement in mathematics. Eurasia Journal of Mathematics, Science and Technology Education, 13(6), 2155-2180.
Zakaria, E., & Syamaun, M. (2017). The effect of realistic mathematics education approach on students’ achievement and attitudes towards mathematics. Mathematics Education Trends and Research, 1(1), 32-40.