Sabtu, 04 Juni 2022
Daya Matematika Menurut Histori, Konsep, Riset, Aplikasi
Rabu, 01 Juni 2022
Daya Matematika Level Filsafat dan Psikologi
A. PENDAHULUAN
Pembelajaran yang baik termasuk pembelajaran matematika adalah pembelajaran yang mencapai tujuannya. Untuk mencapai tujuannya, suatu pembelajaran haruslah bermakna yang dilakukan selain melalui aktivitas juga dengan kegiatan tanya jawab. Kegiatan menanya selain dapat meningkatkan kreativitas dengan kemungkinan memunculkan pertanyaan-pertanyaan dibalik suatu pertanyaan yang membentuk suatu eksponensial, juga mampu mengukur tingkat perhatian siswa dalam pembelajaran. Untuk dapat menanya perlu berbagai informasi yang diketahui dan hal yang hendak dikaitkan atau diuji kebenarannya. Dalam matematika, kemampuan matematika atau daya matematika seseorang berpengaruh pada keberhasilan dalam pembelajaran matematika. Kemampuan matematis didefinisikan oleh NCTM (1999) sebagai kemampuan dalam mengeksplorasi, melakukan konjecture dan argumentasi logis dalam menyelesaikan permasalahan tidak rutin, mengkomunikasikan melalui bentuk matematis dan menghubungkan ide-ide pada matematika dengan disiplin ilmu yang lain. Terdapat banyak komponen dari daya matematika ditinjau dari keilmuannya seperti aljabar, numerik, statistik, kalkulus, geometri, dan sebagainya namun perlu juga diperhatikan aspek filosofis dan psikologisnya.
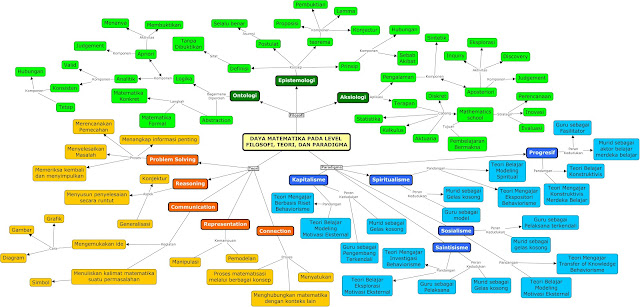
Matematika sebagai suatu keilmuan memiliki objek langsung dan objek tak langsung. Objek langsung meliputi fakta, postulat, aksioma, konsep, prinsip, dan prosedur. Sedangkan obyek tak langsung meliputi kemampuan memecahkan masalah, kemampuan menalar, kemampuan mengkomunikasikan, kemampuan menghubungkan, dan kemampuan representasi. Kemampuan pemecahan masalah meliputi kemampuan memahami konsep dan menggunakan prosedur dalam mencari solusi dari permasalahan matematika. Kemampuan menalar meliputi kemampuan dalam menghubungkan fakta-fakta untuk menarik suatu kesimpulan. Adapun aktivitas yang tercakup di dalam kegiatan penalaran matematik meliputi: menarik kesimpulan logis; menggunakan penjelasan dengan menggunakan model, fakta, sifat-sifat, dan hubungan; memperkirakan jawaban dan proses solusi; menggunakan pola dan hubungan; untuk menganalisis situasi matematik, menarik analogi dan generalisasi; menyusun dan menguji konjektur; memberikan lawan contoh (counter example); mengikuti aturan inferensi; memeriksa validitas argument; menyusun argument yang valid; menyusun pembuktian langsung, tak langsung dan menggunakan induksi matematik.
Sementara itu kemampuan komunikasi matematis (mathematical communication) merupakan kesanggupan atau kecakapan siswa untuk menyatakan dan menafsirkan gagasan matematis secara lisan, tertulis atau mendemonstrasikan apa yang ada dalam persoalan matematika dan juga kemampuan untuk mendemonstrasikan dan manafsirkan gagasan atau ide matematika dari suatu uraian ke dalam model matematika (grafik, diagram, tabel dan persamaan). Kemampuan koneksi matematik adalah kemampuan yang ditunjukkan siswa dalam mengenali representasi ekuivalen dari konsep yang sama, mengenali hubungan prosedur matematika suatu representasi ke prosedur representasi yang ekuivalen, menggunakan dan menilai keterkaitan antar topik matematika dan keterkaitan di luar matematika, menggunakan matematika dalam kehidupan sehari-hari. Kemampuan representasi matematis adalah salah satu standar proses yang perlu ditumbuhkan dan dimiliki siswa.
B. ASPEK FILOSOFIS
Aspek dasar filosofis suatu ilmu termasuk matematika adalah ontologi, epistimologi, dan aksiologi. Setiap metode filosofis memiliki tempat tersendiri dalam kegiatan memecahkan masalah matematika, seperti metode Apriori dan Aposteriori.
1. Metode Apriori
Metode apriori tanpa percobaan dapat digunakan dalam statistik, yakni mengetahui peluang tanpa melakukan percobaan terlebih dahulu. Contoh berapa peluang munculnya kartu king dalam 2 kali pengambilan kartu tanpa pengembalian? Jika diketahui bahwa peristiwa A dapat muncul dalam m cara dan total seluruh kemungkinan peristiwa adalah n, maka peluang munculnya peristiwa A: P(A)=m/n.
2. Metode Aposteriori
Metode aposteriori dapat digunakan dalam statistik seperti pada contoh jika peristiwa serupa A muncul m kali dalam total percobaan n, maka peluang pengamatan P(A)=m/n. Ini berarti diasumsikan percobaan telah dilakukan dengan memperoleh peluang pengamatan. Bila dalam 80 kali pelemparan mata uang (yang tak harus seimbang) munculnya Angka sebanyak 45 kali (sisanya Gambar sebanyak 35 kali), maka P (munculnya Angka) = 45/80. Setelahnya maka menggunakan pengalaman tersebut sebagai dasar dalam menentukan pengalaman baru.
Selain terdapat metode yang dapat diimplementasikan dalam setiap cabang ilmu matematika, dalam aspek filosofis terdapat logika dan pengalaman. Logika memiliki unsur-unsur yakni analitik dan apriori. Unsur analitik saling melengkapi dengan apriori, jika apriori adalah kemampuan mengetahui yang belum terjadi maka analitik disini berfungsi untuk menimbang dan menggali kebenaran dari apriori dengan berbagai hal yang memiliki keterkaitan. Seseorang yang daya matematikanya kuat, logikanya pasti kuat dan analitiknya juga kuat. Sementara itu unsur dari pengalaman adalah sintetik aposteriori. Sintetik dan aposteriori juga saling melengkapi dalam hal saling mengaitkan antara pengetahuan yang telah dimiliki dengan yang baru saja diperoleh melalui hubungan sebab akibat sehingga paham setelah kejadian. Benjamin Bloom telah mengklasifikasikan tingkat kemampuan berpikir seseorang, bahwa sebelum direvisi oleh Anderson (2001) tingkatan tertinggi dalam kemampuan berpikir adalah sintesis lalu diikuti evaluasi. Evaluasi disini bermakna memberikan keputusan atau judgment.
Kemampuan berpikir seseorang ada kaitannya dengan kemampuan memahami realita fenomenologi dimana unsurnya adalah reduksi dan idealisasi. Reduksi adalah kemampuan untuk bisa melihat sedangkan idealisasi adalah kemampuan dalam menyimpulkan. Sebagai contoh seseorang dapat naik kereta api dan melihat fenomena kereta tersebut berjalan cepat atau lambat sehingga dengan membandingkan waktu tempuh naik kereta dengan baik bus dapat disimpulkan mana yang lebih cepat. Dari unsur-unsur logika dan pengalaman, pengaruhnya dalam pembelajaran matematika tentu sangat banyak. Seseorang dengan kemampuan apriori dan analitik yang baik tentu akan dapat sedikit menerawang dan memiliki kemampuan bermain logika dalam pikirannya seperti contoh mengenai mahasiswa yang diajak studi tour ke candi Borobudur lalu diminta melakukan analisa keterkaitannya dengan etnomatematika. Mahasiswa dengan kemampuan apriori yang baik akan segera berpikir mengenai hal apa saja yang perlu dipersiapkan dan diamati lantas dipadukan dengan analitik yang baik berdasarkan aposteriori yang dimiliki untuk menghasilkan suatu sintesis yang baik mengenai keterkaitan etnomatematika dalam bentuk candi borobudur seperti konsep perhitungan volume batu yang digunakan, bentuk arsitektur agar dapat berdiri kokoh di atas bukit, serta bentuk ornamen-ornamen yang memiliki keindahan namun tetap tersusun dengan baik,
Selanjutnya dalam pembelajaran matematika menurut Shigeo Katagiri perlu memperhatikan konten dan metodenya. Setiap konten tentu memiliki metode berbeda untuk mempelajarinya, apakah dengan deduktif atau induktif. Pengemasan konten yang menarik dengan metode yang sesuai akan dapat membuat siswa lebih mudah dalam mempelajari sehingga memiliki kontribusi besar pada daya matematika yang dimiliki siswa. Komponen matematika yang terdiri dari Fakta, Postulate, Aksioma, Teorema, Prinsip memiliki cara-cara dalam mengajarkannya. Salah satunya adalah dengan pendekatan Realistik yang membawa matematika dari aspek konkret menuju formal dengan fenomena didaktis di dalamnya. Dalam tahapan mempelajarinya perlu conjecture dan convince menurut Profesor Kaye Stacey yakni hubungan yang logis dan dapat dibuktikan.
C. ASPEK PSIKOLOGIS
Dari aspek psikologi, kemampuan seseorang dalam mengolah informasi itu berbeda-beda termasuk di dalamnya terdapat strategi agar mudah mengingat atau menyimpan informasi seperti dengan membuat skema-skema atau singkatan-singkatan, namun juga terdapat faktor lupa. Salah satu hal penting dalam aspek psikologi belajar adalah perhatian dan hubungan antara pengetahuan awal dan informasi baru. Perhatian akan membantu seseorang untuk fokus pada 1 hal, karena manusia tidak dapat fokus dalam banyak hal sekaligus. Selain itu, dengan materi yang terlalu banyak seseorang dapat mengalami cognitive overload walaupun dalam beberapa fakta mengatakan seseorang yang berdaya matematika kuat maka memiliki perhatian dan ketahanan belajar yang kuat pula.
DAYA MATEMATIKA: Pendahuluan
Daya matematika yakni mathematical power yang berbeda dengan power of mathematics. Daya matematika tidak dapat dilepaskan dari filsafat ilmu yakni pada aspek ontologi (makna), aspek epistemologi (cara mempelajarinya), dan aspek aksiologi (kebermanfaatan suatu ilmu). Daya matematika atau mathematical power diibaratkan sebagai titik tengah di antara hulu dengan hilir yang dapat menentukan apakah seseorang yang belajar ilmu matematika (hulu) dapat mencapai tujuan dari belajar matematika tersebut (hilir). Daya matematika mencakup pengetahuan akan makna dari ilmu matematika, strategi mempelajari dan memecahkan masalah, serta mampu menggali potensi dari ilmu matematika yang merupakan power of mathematics.
Sebagai contoh dari power of mathematics adalah terciptanya alat bantu hitung dari suatu algoritma yakni kalkulator dan komputer, terciptanya berbagai alat elektronik dan otomotif berdasarkan perhitungan yang mengkombinasikan fisika dan matematika, terciptanya berbagai macam obat atau antivirus yang mencegah perkembangbiakan virus secara cepat dan berkelipatan. Daya matematika adalah suatu potensi yang dimiliki oleh setiap orang dalam hal memperoleh ilmu matematika dan menjadi ahli untuk menerapkan keilmuan tersebut di dalam kehidupan sehari-hari. Untuk memiliki daya matematika tentu dapat dengan melatih literasi matematika seperti kemampuan memecahkan masalah, menalar, komunikasi, dan menghubungkan. Melatih literasi matematika dapat melalui pendugaan dan penemuan, mengajukan suatu permasalahan atau pertanyaan, maupun eksplorasi.
Pada aspek kemampuan memecahkan masalah, seseorang dapat dibimbing dalam hal melihat informasi yang berkaitan dengan apa yang ditanyakan berdasarkan teori Vygotsky mengenai Zona Proximal Development yakni berdasarkan tingkat kebutuhan bantuan sampai dapat mandiri memecahkan suatu permasalahan. Akan lebih baik apabila permasalahannya bukan hal yang rutin. Pada aspek menalar, seseorang dapat dilatih dengan tipe soal berbasis High Order Thinking Skill (HOTS) sehingga dapat menganalisa, mengevaluasi, bahkan menciptakan hal baru dari suatu hal. Pada aspek komunikasi, seseorang dapat dilatih untuk mengemukakan ide atau mengkonstruksi bentuk matematis dari suatu langkah penyelesaian masalah. Pada aspek menghubungkan, seseorang dapat dilatih dengan berbagai permasalahan yang saling memiliki keterkaitan baik berbagai subyek dalam suatu ilmu maupun berbagai subyek dari berbagai keilmuan yang berbeda.
Sebagai pendukung dalam upaya meningkatkan daya matematika seseorang, pemilihan sumber belajar juga harus diperhatikan agar dapat memfasilitasi aktivitas. Perbantuan media belajar seperti Augmented Reality, video pembelajaran, aplikasi seperti GeoGebra, Autograph, Desmos dapat membantu siswa dalam melatih kemampuan visualisasi dari suatu konsep seperti Geometri, Kalkulus, Aritmatika, Statistika, dan lain sebagainya. Penggunaan alat bantu perhitungan juga diharapkan dapat membuat siswa berlatih untuk mempertajam kemampuan berpikir kritis dan kreatif.